It may come as no surprise that 75% of the students featured in the video were unable to reason their way through the shepherd problem. EQAO scores have hit a new low under the latest Ontario math curriculum, and the Ministry is pushing for renewed strategies that include mandated daily math instruction and the designation of a math lead teacher at each school to help fix this.
While some will quickly identify inquiry-based learning and the new curriculum as the root cause of the decline in test scores, EQAO assessment remains rooted in the closed-ended questions of years gone by and is at odds with how math has been taught recently. It should therefore come as no surprise that students are not succeeding when blindsided by problem sets unlike anything they have seen before.
It is clear that there exists a disconnect between knowing math and understanding math, and it takes no more than a quick show of hands for one to find that people think it is more important to understand math than to know it. This is representative of the shift in mindset that has been occurring in recent years with respect to mathematics education, however this push for renewed mindsets is contradicted by demands for standardized testing and rote mathematical skills. How will students achieve if parents do not value the new methods of mathematics instruction?

Last year a simple math problem marked as incorrect sent the internet into a furor. People quickly came to the defense of the student, pointing out that five times three and three times five had the same solution that we all know as 15. The article however, parsed the definition of multiplication, defending the teacher and their professional judgement.
5 x 3 = 3 + 3 + 3 + 3 + 3
As much as I was raised to respect and think in terms of the strict rules of mathematics, this aspect of multiplication was never harped upon. Sure, if you write it as you would teach it for primary students you would have five groups of three, which is indeed what the definition puts forth. This however ignores the fact that students have traditionally learned multiplication with the help of tables (hence times tables), and that one can quickly notice certain trends with the help of such tools.

The commutative property of multiplication is certainly apparent through the use of such tools, as it would be if students were simply expected to memorize the values of each product. While five groups of three and three groups of five are certainly distinct from one another, I vehemently disagree with the teacher's actions. Context is important in mathematics, and while we do not know if the student had learned previously the commutative property of multiplication, there is no context guiding the question in such a way that the distinction is important.
a x b = b x a
Consider the array the student drew in the next question. I see four groups of six and six groups of four, and we cannot know for certain that the student did not count the groups vertically instead of horizontally as the teacher insisted. At this point I feel the teacher is leading the student astray and sticking to a very traditional mindset, telling the student that there is only one way to solve a math problem. A 4x6 and a 6x4 array are identical without some sort of guiding parameters---for example, a fence that is four feet wide and six feet tall is distinct from a fence that is six feet wide and four feet tall---and rather than penalizing the student, it would be an excellent opportunity to ask deeper why or how questions to probe for understanding.

Approaching multiplication from an inquiry- or exploration-based approach, we must tread carefully around such scenarios. Students will quickly discover the commutative property on their own, and may use this to simplify problems and make their lives easier. I certainly would not go about multiplying 5 x 3 by adding five threes when I could much more easily add three fives. It's a shortcut, a mental math strategy of dissecting a question in a way that makes it simpler, and we should be happy to see students drawing such connections and discovering these relationships.
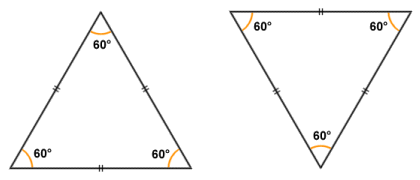
Are these triangles congruent if one is upside-down?
While some will quickly identify inquiry-based learning and the new curriculum as the root cause of the decline in test scores, EQAO assessment remains rooted in the closed-ended questions of years gone by and is at odds with how math has been taught recently. It should therefore come as no surprise that students are not succeeding when blindsided by problem sets unlike anything they have seen before.
It is clear that there exists a disconnect between knowing math and understanding math, and it takes no more than a quick show of hands for one to find that people think it is more important to understand math than to know it. This is representative of the shift in mindset that has been occurring in recent years with respect to mathematics education, however this push for renewed mindsets is contradicted by demands for standardized testing and rote mathematical skills. How will students achieve if parents do not value the new methods of mathematics instruction?

Last year a simple math problem marked as incorrect sent the internet into a furor. People quickly came to the defense of the student, pointing out that five times three and three times five had the same solution that we all know as 15. The article however, parsed the definition of multiplication, defending the teacher and their professional judgement.
As much as I was raised to respect and think in terms of the strict rules of mathematics, this aspect of multiplication was never harped upon. Sure, if you write it as you would teach it for primary students you would have five groups of three, which is indeed what the definition puts forth. This however ignores the fact that students have traditionally learned multiplication with the help of tables (hence times tables), and that one can quickly notice certain trends with the help of such tools.

The commutative property of multiplication is certainly apparent through the use of such tools, as it would be if students were simply expected to memorize the values of each product. While five groups of three and three groups of five are certainly distinct from one another, I vehemently disagree with the teacher's actions. Context is important in mathematics, and while we do not know if the student had learned previously the commutative property of multiplication, there is no context guiding the question in such a way that the distinction is important.
Consider the array the student drew in the next question. I see four groups of six and six groups of four, and we cannot know for certain that the student did not count the groups vertically instead of horizontally as the teacher insisted. At this point I feel the teacher is leading the student astray and sticking to a very traditional mindset, telling the student that there is only one way to solve a math problem. A 4x6 and a 6x4 array are identical without some sort of guiding parameters---for example, a fence that is four feet wide and six feet tall is distinct from a fence that is six feet wide and four feet tall---and rather than penalizing the student, it would be an excellent opportunity to ask deeper why or how questions to probe for understanding.

Approaching multiplication from an inquiry- or exploration-based approach, we must tread carefully around such scenarios. Students will quickly discover the commutative property on their own, and may use this to simplify problems and make their lives easier. I certainly would not go about multiplying 5 x 3 by adding five threes when I could much more easily add three fives. It's a shortcut, a mental math strategy of dissecting a question in a way that makes it simpler, and we should be happy to see students drawing such connections and discovering these relationships.

Are these triangles congruent if one is upside-down?
